CFD

Computational Fluid Dynamics (CFD) simulations performed with the open source SU2 CFD code [1] and other custom-written codes in C++.

2D NACA 0012 case

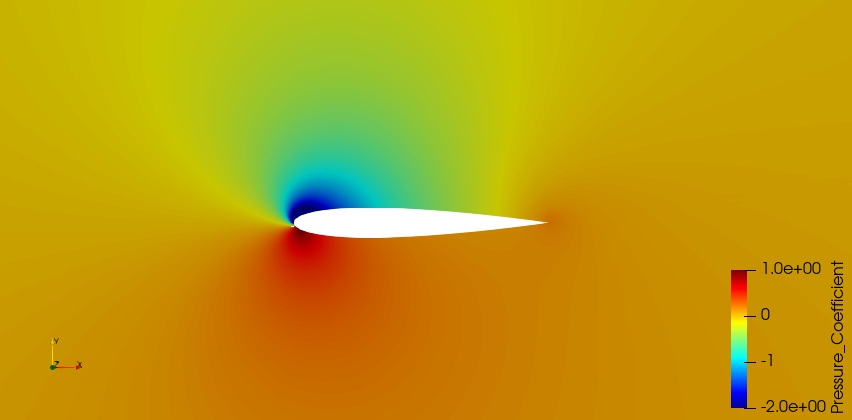
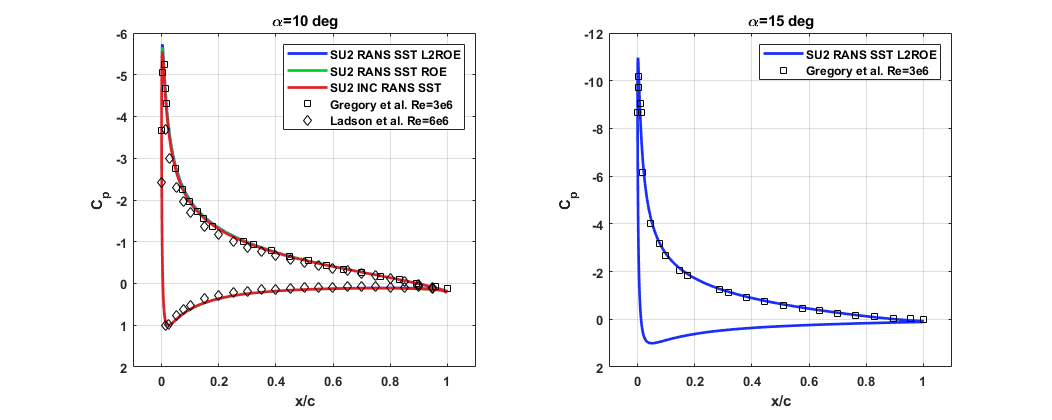
Two dimensional simulations of a NACA0012 airfoil at a Reynolds number of 6 million and 10 deg AOA were performed using the k-ω SST turbulence model. The results from the SU2 incompressible and compressible solvers were compared. The MUSCL approach was used to provide 2-nd order accuracy in space in combination with the Venkatakrishnan slope limiter. The effect of the discretisation scheme on the convective fluxes was also investigated. For the compressilbe solver a standard non-dimensionalisation was used where the reference pressure is chosen such that the non-dimensional free-sream velocity equals 1. Results were compaired against the experiments reported in [2,3].

From the pressure coefficient distribution it was observed that both the incompressible and compressible SU2 solvers are in good agreement with the experimental results. No significant differences were observed between the two discretisation schemes - ROE and L2ROE. Nevertheless for Mach numbers less than 0.1 one should consider the L2ROE scheme or another low Mach scheme if using the compressible SU2 solver.

NACA 4412 wing case

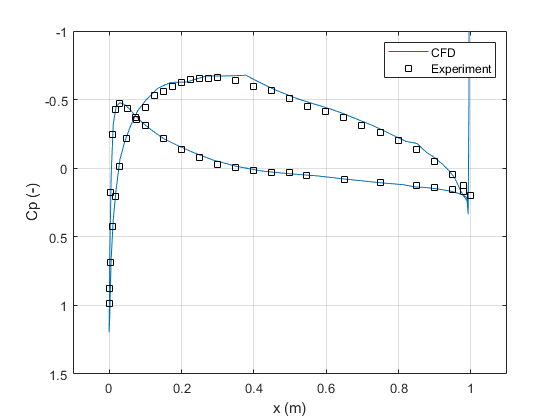
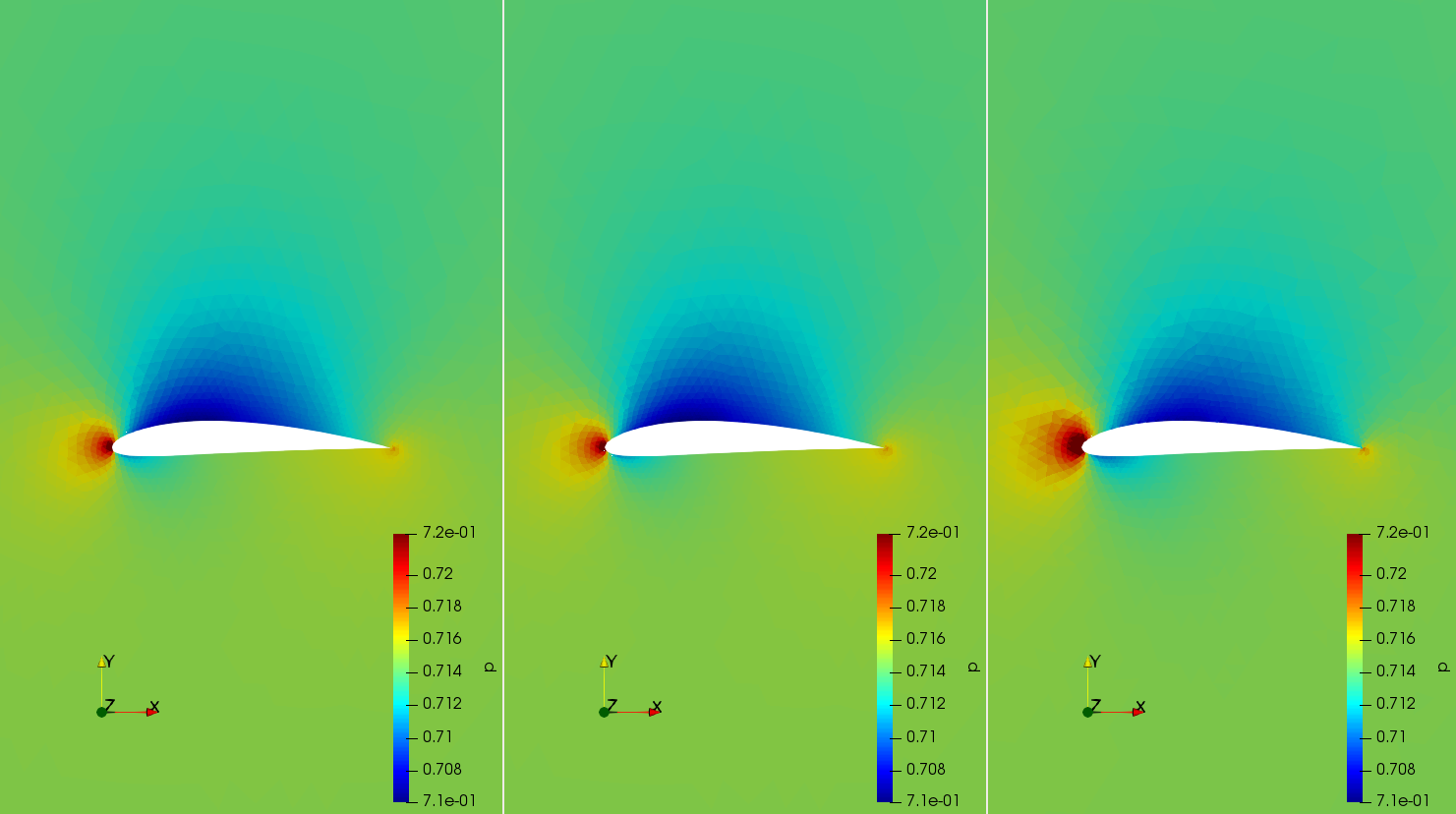
Three-dimensional simulations of a NACA4412 wing of AR=6 at 0 deg AOA were performed on a hybrid (structured-unstructured) mesh with the k-ω SST turbulence model. The flux difference splitting (FDS) scheme with low speed preconditioning is used for descretisation of convective fluxes and the MUSCL approach is used to provide 2nd-order accuracy in space in combination with the Venkatakrishnan slope limiter. The standard non-dimensionalisation is used. The results from the 2D simulations were compaired against the experiments reported in [4].

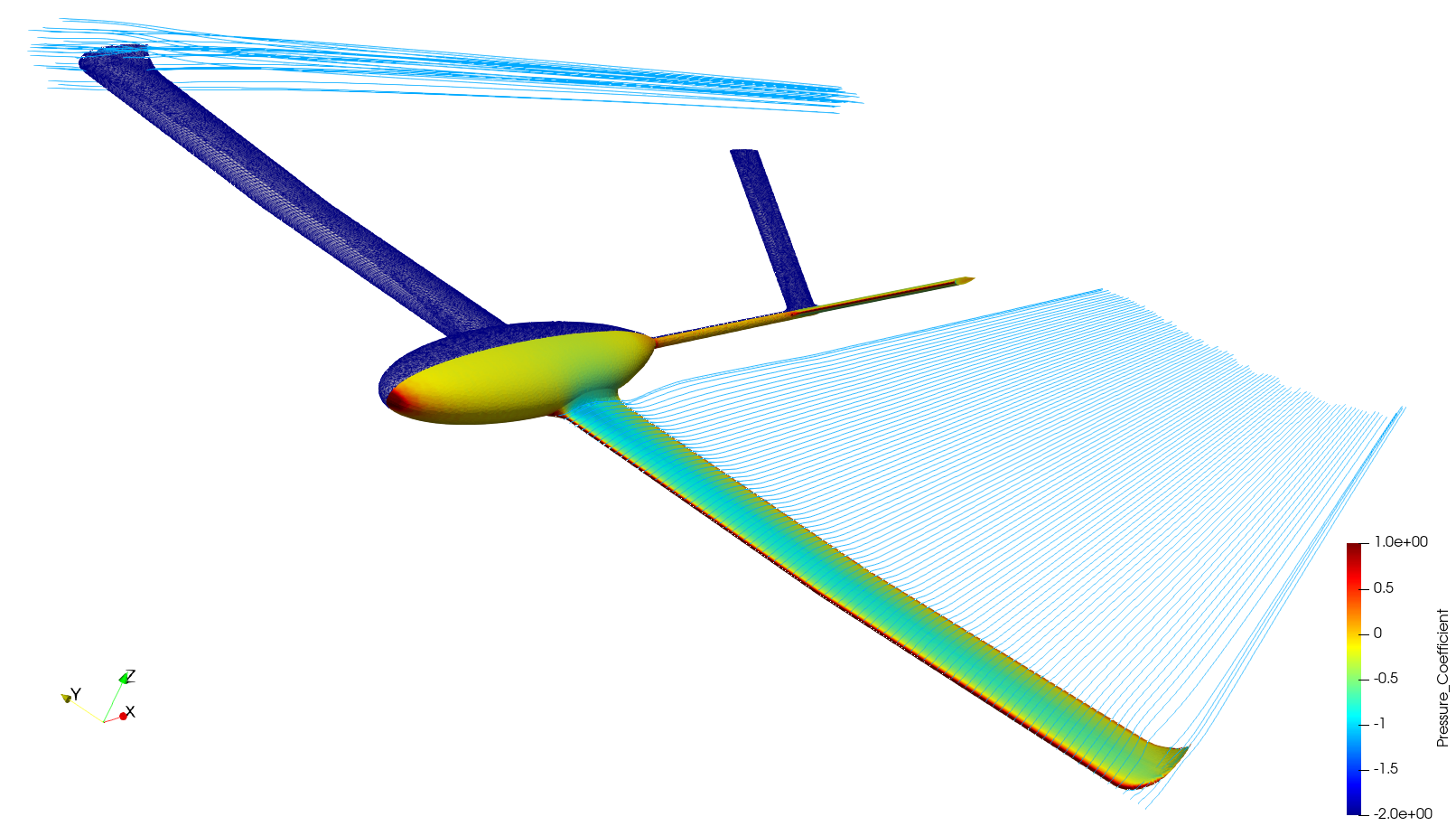
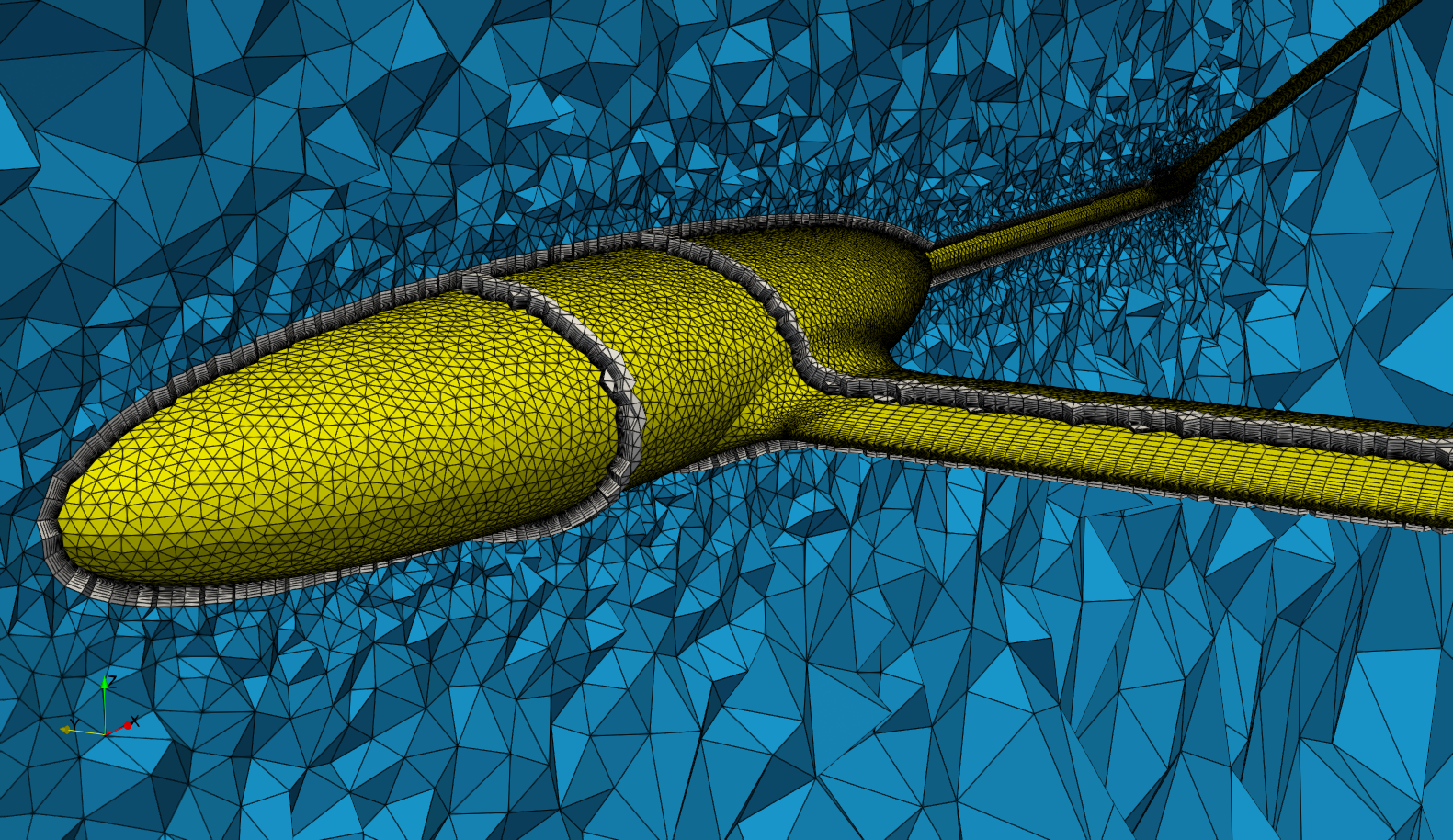
UAV case

Three-dimensional simulations of a fixed-wing UAV at 0 deg AOA and 0 deg AOS featuring NACA4412 and NACA0012 airfoils were performed on a hybrid (structured-unstructured) mesh with the k-ω SST turbulence model. The flux difference splitting (FDS) scheme with low speed preconditioning is used for descretisation of convective fluxes and the MUSCL approach is used to provide 2nd-order accuracy in space in combination with the Venkatakrishnan slope limiter. The standard non-dimensionalisation is used. Symmetry across the z-x plane is enforced. The total number of mesh elements is around 4 million (coarse mesh). The simulation time required for convergence of the aerodynamic loads was approximately 3 hours. The simulation was run on the Google Compute Engine on a c2-standard-16 instance.

ONERA bump case

Two-dimensional simulation of the ONERA bump performed on a structured mesh with the k-ω SST turbulence model. The Roe scheme is used for discretisation of the convective fluxes and the MUSCL approach is used to provide 2-nd order accuracy in space in combination with the Venkatakrishnan slope limiter. A standard non-dimensionalisation is used where the reference pressure is chosen such that the non-dimensional free-sream velocity equals 1. The results from the 2D simulations were compaired against the experiments reported in [5].

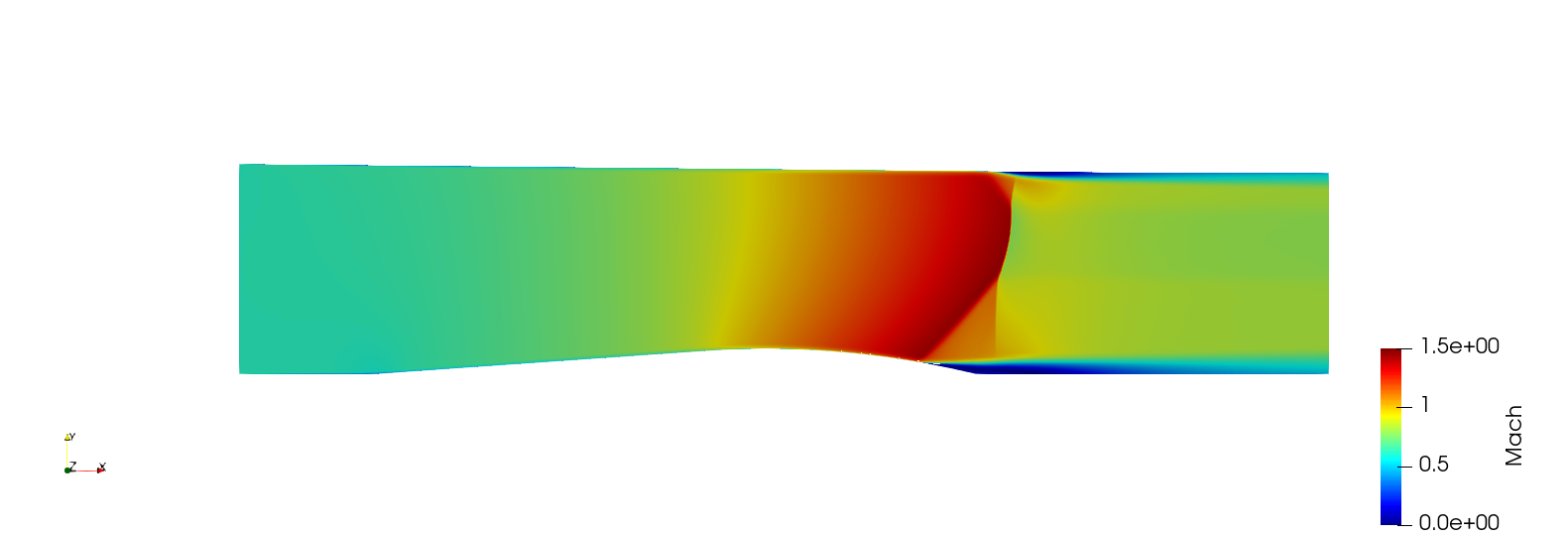
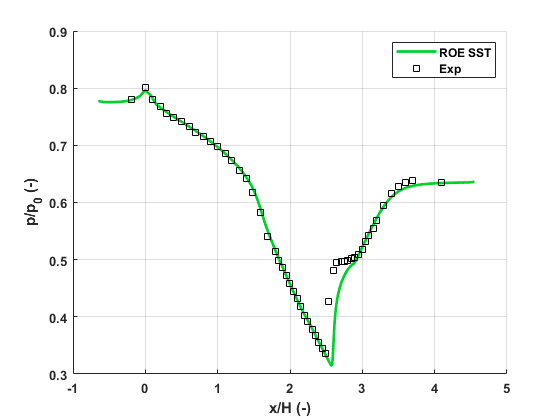
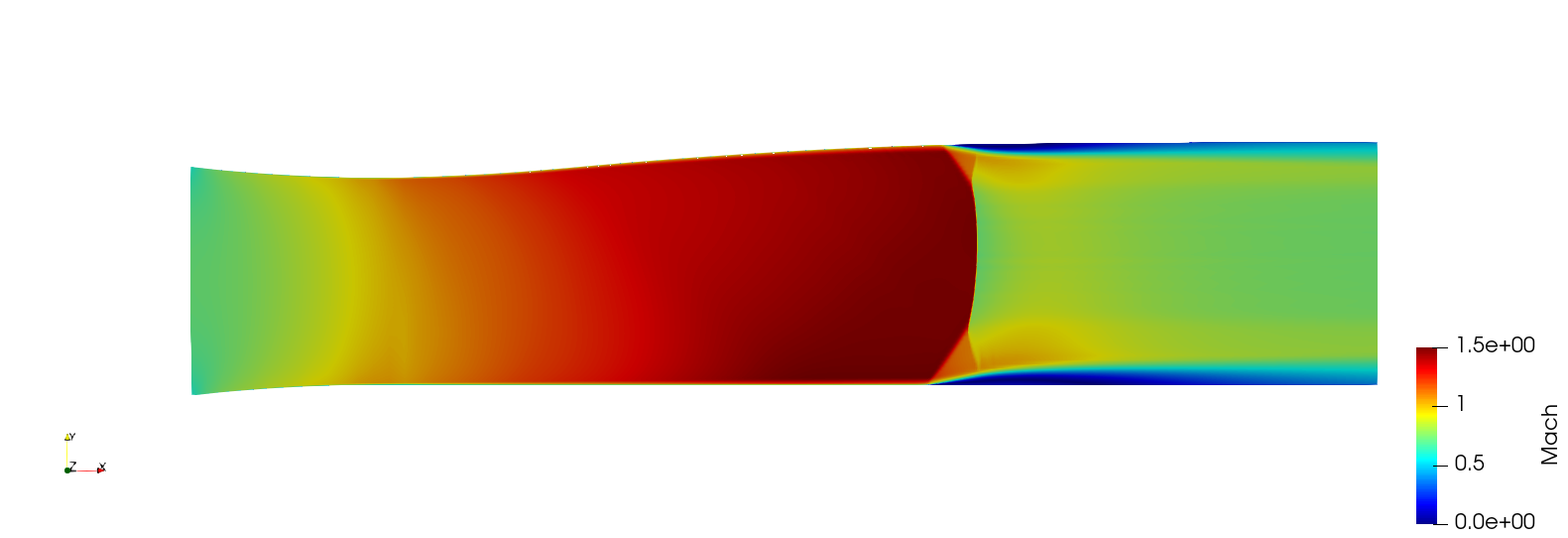
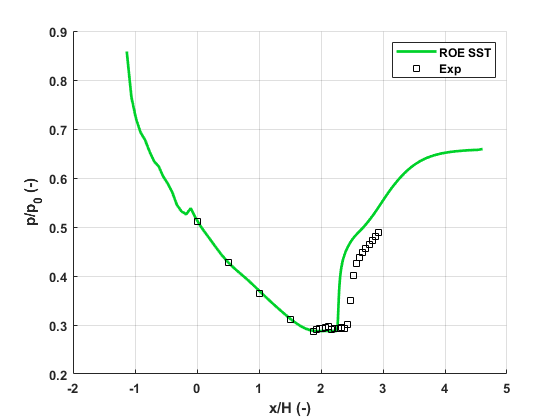
IMP nozzle case

Two-dimensional simulation of the IMP normal shock experiment performed on a structured mesh with the k-ω SST turbulence model. The Roe scheme is used for discretisation of the convective fluxes and the MUSCL approach is used to provide 2-nd order accuracy in space in combination with the Venkatakrishnan slope limiter. A standard non-dimensionalisation is used where the reference pressure is chosen such that the non-dimensional free-sream velocity equals 1. The results from the 2D simulations were compaired against the experiments reported in [6-8].

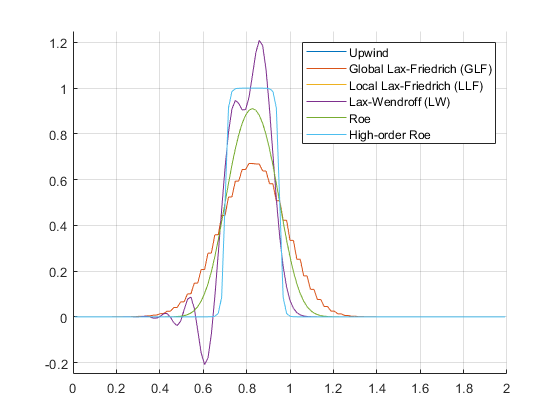
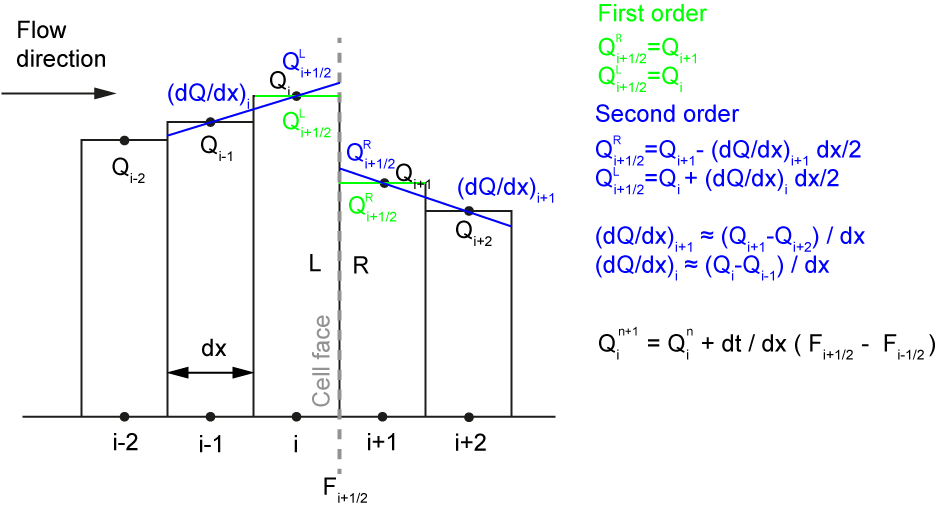
FVM for 1D advection equationA FVM MATLAB code solving the 1D advection eqation with different numerical schemes. The
                    available numerical schemes are:
                
Upwind
Global Lax-Friedrichs
Local Lax-Friedrichs
Lax-Wendroff
Roe
High-order Roe

                Different limiters are available for the high-order Roe scheme. High-order is achieved by linear
                extrapolation of the cell variables to the cell faces. For the 1D advection equation, the Upwind, Local
                Lax-Friedrich, and Roe schemes give the same solution. Please refer to the schematic on the right for
                more information.
                
fvm_1d_advection.m

FVM for shallow water equations

A unstructured finite volume method (FVM) shallow water solver written in C++. Fluxes can be evaluated with the Lax-Friedrichs or the Roe method. Implicit and explicit time stepping is available. Expicit time stepping can be performed with the Euler, the Runge-Kutta 2nd-order, and the Runge-Kutta 4th-order methods. The jacobian used for the implicit time stepping is numerically evaluated and the linear system of equations is solved with the BiCGSTAB method. The Eigen C++ template library for linear algebra is used along with OpenMP. The C++ code is available at https://github.com/KBoychev/fvm_shallow_water. The animations below show the water height of a dam break problem.

FVM for Euler equations

A 2D unstructured finite volume method (FVM) Euler solver written in C++. Fluxes can be evaluated with the Lax–Friedrichs or the Roe method. Explicit pseudo-time stepping is available. Expicit pseudo-time stepping can be performed with the Euler, the Runge-Kutta 2nd-order, and the Runge-Kutta 4th-order methods. The Eigen C++ template library for linear algebra is used along with OpenMP. The C++ code is available at https://github.com/KBoychev/fvm_euler. The figure below shows the pressure around a NACA4412 airfoil with the Roe and RK2 methods (left), the Roe and RK4 methods (middle), and the Lax-Friedrichs and Euler methods (right).

References

[1] F. Palacios, M. R. Colonno, A. C. Aranake, A. Campos, S. R. Copeland, T. D. Economon, A. K. Lonkar, T. W. Lukaczyk, T. W. R. Taylor, and J. J. Alonso. Stanford University Unstructured (SU2): An open-source integrated computational environment for multi-physics simulation and design. AIAA Paper 2013-0287, 51st AIAA Aerospace Sciences Meeting and Exhibit, January 2013.
[2] N. Gregory and C. L. O'Reilly. Low-speed aerodynamic characteristics of naca 0012 aerofoil sections, including the effects of upper-surface roughness simulation hoar frost. NASA R & M 3726, 1970.
[3] C. Ladson and A. Hill and W. Johnson. Pressure distributions from high Reynolds number transonic tests of an NACA 0012 airfoil in the Langley 0.3-meter transonic cryogenic tunnel. NASA TM 100526, 1987.
[4] Pinkerton, R. M. "Calculated and measured pressure distributions over the midspan section of the N.A.C.A 4412 airfoil", 1936.
[5] J.M. Delery. Experimental Investigation of Turbulence Properties in Transonic Shock/Boundary-Layer Interactions. AIAA Journal, 21(2):180–185, 1983.
[6] P. Doerffer, O. Szulc, and F. Magagnato. UNSTEADY SHOCK WAVE - TURBULENT BOUNDARY LAYER INTERACTION IN THE LAVAL NOZZLE. TASK QUARTERLY, 9(1):115–132, 2004.
[7] P. Doerffer, O. Szulc, and F. Magagnato. Shock Wave-Boundary Layer Interaction in Forced Shock Oscillations. Journal of Thermal Science, 12(1):10–15, 2003.
[8] P. Doerffer, C. Hirsch, J.P. Dussauge, H. Babinsky, and Barakos G.N. Unsteady Effects of Shock Wave Induced Separation. In Notes on Numerical Fluid Mechanics and Multidisciplinary Design, 2011.

Back to: About